Prudential Harnesses the Wisdom of Crowds

“Statistics is boring! I can prove it to you!” I sometimes declare in statistics classes that I teach. I do that in order to make the class lively. As proof, I ask the class to name a famous physicist (Einstein's name comes up every time), a famous biologist (Darwin's name comes up every time), and so on. I finally, ask them to name a famous statistician. This is usually greeted with silence, laughter, and the inevitable smart aleck response, “Shashi.” Statistics has no celebrities to boast of? It must be boring! Is it really? I proceed to challenge the class with “I bet you definitely know the name of a famous and pioneering statistician.” This is indeed true, but the class has to wait till the end of the day to know who it is.

I often try to make up simple experiments to help the class realize that statistics is merely common sense quantified. Sadly, this is not the message most people take away from statistics classes or training that they might have endured. So, I was quite struck by the uniqueness of the Prudential commercial demonstrating statistics in an interactive way. In this commercial, filmed at a park in Austin, Texas, a group of 400 people were asked the question “How old is the oldest person you've ever known?” Each person was given a blue dot and asked to stick it on a 1,100-square-foot wall, lined up with the age of that person. The results, and the way the results develop into a neat histogram, are striking.

A participant in Prudential's commercial adds her sticker.
The final array of stickers is on the right.

The visual effect is spectacular because the blue dots organically pile up into a mountain well to the right of a reference line showing the retirement age of 65. Prudential prudently realized that the public cannot be expected to show sustained interest in static graphs or percentages (even when rendered in arresting, moving colors and fonts) attempting to communicate details of life expectancy and the cost of retirement. In a refreshing move, they harnessed the wisdom of the crowds to create a compelling visual for them.

Compelling, it is. But the thought that is so compellingly communicated – “Oh my gosh! Just look at this huge number of very very old people! If they retired at 65, what in the world are they going to live on in their 90s and beyond? Now, I better do something about this for myself!” – is quite far removed from the statistical facts that happen to be actually relevant to retirement and ageing.

Besides, there is a bit of a problem with the question “How old is the oldest person you've ever known?” This was revealed when I attempted to duplicate the experiment using my friends as volunteers: Given more time to think and more opportunity for family members to jog our memory, we often find that we have known someone older than what we first thought. And, as it often happened in my experiment, we can recall knowing someone really old without knowing their exact age. A statisticians job is to prevent such problems by helping develop a solid protocol for the experiment.

But never mind. I don't want this blog to turn out to be a critique of Prudential’s approach to selling retirement planning products. On the contrary, I very much appreciate Prudential’s effort in bringing complex statistical concepts to the masses. In fact, a number of interesting statistical and computational ideas can be illustrated by taking Prudential’s experiment as a starting point. Let us explore.

First, let us try to quantitatively describe shape of the mountain of blue stickers. Since it looks suggestive of the famous bell curve, let us fit such a curve to approximate the tops of the stacks of blue stickers. The blue sticker experiment’s design – and the resulting images – actually makes it easy for us to fit a bell curve. The steps are easy: (1) Scan each column of pixels in the image from top to bottom and place a red mark at the first blue pixel encountered. (2) Next, allow a curve fitting algorithm (quite routinely used in scientific programming) to find the bell curve that best follows the red marks. The figure below shows the steps and the result of doing this exercise involving simple image processing and curve fitting operations.

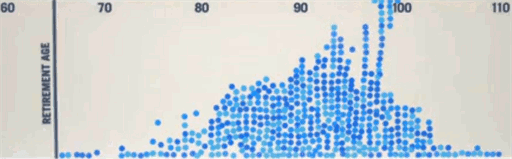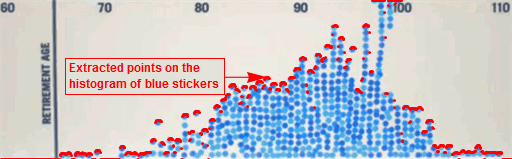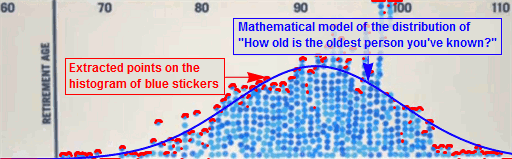Fitting a bell curve to the histogram of blue stickers

Next we ask questions. “Why does the mountain of blue stickers have the appearance that it does? Why does it look orderly even though the participants did not plan for creating the order? Why does it have a peak around 90 years?” We can answer these questions by doing our own blue sticker experiment, this time virtually (and at near-zero cost!)

Let us start with the 2011 US Census, which makes data on age distribution available on its website. From this data, we can apply curve fitting again to build an approximate mathematical model of age distribution, shown as the blue curve which approximately follows the red data points.

Age distribution data and its mathematical model

Having a mathematical model allows us to perform all manner of useful thought experiments, or simulations – or indulge our fancy. When done carefully, these experiments give rise to insight, help make predictions and often provide easy answers to real world questions. For example, from the mathematical model of age distribution, we can generate a random group of virtual people and be sure that the number of retirees (i.e. those past 65) is about what would be expected in an actual sample of the same size (roughly 12%). We can then create an easily understandable picture of the age distribution of that group.

A random group of virtual people. Those aged 65 and older are colored orange.

If I were a participant in Prudential’s experiment and if the people depicted in this picture were the ones (and only ones) ever known to me, I would go up to the wall and place my sticker above the 92 mark. How old is the oldest person you've ever known? 92.

Since we have a mathematical model, we can repeat this process of identifying the oldest individual as often as we like, each time using a different virtual group. Each repetition of the process corresponds to one instance of an individual in Prudential’s experiment mentally going over everyone ever known to him or her and identifying the oldest person known. The result of repeating the process a large number of times – each time placing a virtual sticker on a virtual wall – is shown in the figure below.

Virtual blue stickers generated by running a simulation of Prudential's experiment.
The histogram and the bell curve fit closely follow the result from the live experiment.

Even though the experiment involves generating random ages, we see that the pattern of stickers is not quite random. It follows what seems to be the familiar bell curve again (shown as a blue curve). What is more, it even peaks at around 90 years. The agreement between the actual (shown as a black dashed curve) and virtual versions is quite close. In aggregate, a predictable pattern emerges from randomness. The wisdom of the crowd ensures that the stickers fall into an orderly and familiar histogram, rather than be scattered all over the place.

So, that’s it for now. I hope we see more such creative attempts to infuse freshness into commercials. Everyone I know enjoyed this commercial. I am sure there were statisticians behind the scene who worked hard, (well before the experiment was conducted live) to make sure that it did not turn out to be a public flop. There is lots more material than can be covered in this blog. Does it really follow a bell curve? Does it matter? What is the distribution that is actually relevant to funding retirement plans?

As always, I will enjoy talking to you about this or any other numerical and insightful topics.