“Statistics
is boring! I can prove it to you!” I sometimes declare in statistics classes that I teach. I do that in order to make the class lively. As proof, I ask the
class to name a famous physicist (Einstein's name comes up every time), a famous biologist
(Darwin's name comes up every time), and so on. I finally, ask them to name a famous
statistician. This is usually greeted with silence, laughter, and the
inevitable smart aleck response, “Shashi.” Statistics has no celebrities to boast of? It must be boring! Is it really? I proceed to challenge the class
with “I bet you definitely know the name of a famous and pioneering
statistician.” This is indeed true, but the class has to wait till the end of the
day to know who it is.
I often try
to make up simple experiments to help the class realize that statistics is
merely common sense quantified. Sadly, this is not the message most people take
away from statistics classes or training that they might have endured. So, I
was quite struck by the uniqueness of the Prudential commercial demonstrating statistics in an interactive way. In this commercial, filmed at a park in
Austin, Texas, a group of 400 people were asked the question “How old is the
oldest person you've ever known?” Each person was given a blue dot and asked to
stick it on a 1,100-square-foot wall, lined up with the age of that person. The
results, and the way the results develop into a neat histogram, are striking.
 |
| A participant in Prudential's commercial adds her sticker. The final array of stickers is on the right. |
The visual effect is spectacular because the blue dots organically pile up into a mountain well to the right of a reference line showing the retirement age of 65. Prudential prudently realized that the public cannot be expected to show sustained interest in static graphs or percentages (even when rendered in arresting, moving colors and fonts) attempting to communicate details of life expectancy and the cost of retirement. In a refreshing move, they harnessed the wisdom of the crowds to create a compelling visual for them.
Compelling,
it is. But the thought that is so compellingly communicated – “Oh my gosh! Just
look at this huge number of very very old people! If they retired at 65, what
in the world are they going to live on in their 90s and beyond? Now, I better
do something about this for myself!” – is quite far removed from the
statistical facts that happen to be actually relevant to retirement and ageing.
Besides, there is a bit of a problem with the question
But never
mind. I don't want this blog to turn out to be a critique of Prudential’s approach
to selling retirement planning products. On the contrary, I very much
appreciate Prudential’s effort in bringing complex statistical concepts to the
masses. In fact, a number of interesting statistical and computational ideas
can be illustrated by taking Prudential’s experiment as a starting point. Let
us explore.
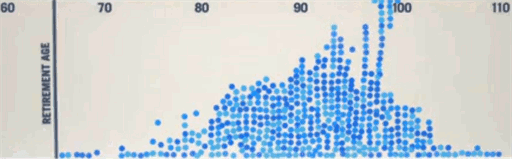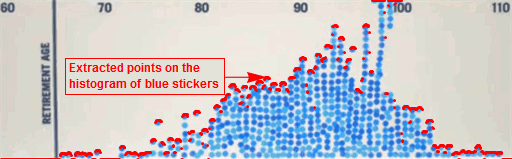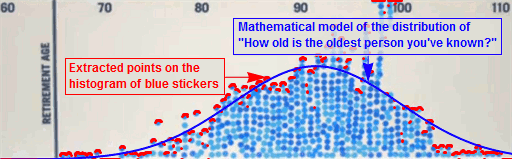 |
| Fitting a bell curve to the histogram of blue stickers |
Next we ask
questions. “Why does the mountain of blue stickers have the appearance that
it does? Why does it look orderly even though the participants did not plan for creating the order? Why does it have a peak around 90 years?” We can answer these questions by doing our own blue sticker experiment, this time virtually (and at near-zero cost!)
Let us start with the 2011 US Census, which
makes data on age distribution available on its website. From this data, we can apply curve fitting again to build an approximate mathematical model of age distribution, shown as the blue
curve which approximately follows the red data points.
 |
| Age distribution data and its mathematical model |
Having a
mathematical model allows us to perform all manner of useful thought experiments,
or simulations – or indulge
our fancy. When done carefully, these experiments give rise to insight,
help make predictions and often provide easy answers to real world questions. For
example, from the mathematical model of age distribution, we can generate a random
group of virtual people and be sure that the number of retirees (i.e. those
past 65) is about what would be expected in an actual sample of the same size (roughly 12%). We
can then create an easily understandable picture of the age distribution of
that group.
Since we have a mathematical model, we can
repeat this process of identifying the oldest individual as often as we like, each time using a different virtual group. Each repetition of the process
corresponds to one instance of an individual in Prudential’s experiment
mentally going over everyone ever known to him or her and identifying the
oldest person known. The result of repeating the process a large number of
times – each time placing a virtual sticker on a virtual wall – is shown in the
figure below.
 |
| A random group of virtual people. Those aged 65 and older are colored orange. |
If I were a
participant in Prudential’s experiment and if the people depicted in this
picture were the ones (and only ones) ever known to me, I would go up to the
wall and place my sticker above the 92 mark. How old is the oldest person you've ever known? 92.
 |
| Virtual blue stickers generated by running a simulation of Prudential's experiment. The histogram and the bell curve fit closely follow the result from the live experiment. |
Even though
the experiment involves generating random ages, we see that the pattern of stickers is
not quite random. It follows what seems to be the familiar bell curve again
(shown as a blue curve). What is more, it even peaks at around 90 years. The
agreement between the actual (shown as a black dashed curve) and virtual
versions is quite close. In aggregate, a predictable pattern emerges from
randomness. The wisdom of the crowd ensures that the stickers fall into an orderly and familiar histogram, rather than be scattered all over the place.
So, that’s
it for now. I hope we see more such creative attempts to infuse freshness into
commercials. Everyone I know enjoyed this commercial. I am sure there were statisticians behind the scene who worked hard, (well before the experiment was conducted live) to make sure that it did not turn out to be a public flop. There is lots more
material than can be covered in this blog. Does it really follow a bell curve? Does
it matter? What is the distribution that is actually relevant to funding
retirement plans?
As always, I will enjoy talking to you about this or any other numerical and insightful topics.